In der heutigen Unternehmenswelt ist es wichtig, dass Sie ein tiefes Verständnis über Ihre Kunden entwickeln. Anhand intelligenter Kundensegmentierungen durch eine Cluster-Analyse, können Sie das Verhalten Ihrer Kunden korrekt einschätzen und daraufhin konkrete Marketingkampagnen ableiten.
Sie wollen das Verhalten Ihrer Kunden genauer verstehen? Anhand einer Kundensegmentierung durch eine Cluster-Analyse, können Sie einfach Kundengruppen bilden, die sich im Verhalten sehr ähneln.
Wir nutzen die Ergebnisse von Kundensegmentierungen, um personalisierte Segmentierungen zu erstellen, die wir anschließend für Marketingkampagnen nutzen. Die Praxis zeigt, dass je genauer Sie Marketingkampagnen auf Ihre Kunden abstimmen, desto höher ist auch der zu erwartende Umsatz pro Kampagne.
Wenn Sie wissen wollen wie Sie den Wert Ihrer Kundenbasis steigern, dann zeige ich Ihnen jetzt, wie Sie eine Sie eine Kundensegmentierung mit einer Cluster-Analyse in Python umsetzen.
Steigen wir direkt ein:
- Kundensegmentierung mit einer Clusteranalyse
- Der Datensatz
- K-Means-Algorithmus einfach erklärt
- Beispiel: Clusterbasierte Kundensegmentierung mit Python
Kundensegmentierung mit einer Clusteranalyse
In diesem Artikel zeige ich, wie eine Kundensegmentierung mit einem Clustering-Algorithmus (Clusteranalyse) erstellt wird. Für diesen Anwendungsfall des maschinellen Lernens haben wir Kundendaten aus einem E-Commerce Shop zur Verfügung.
Wenn Sie genauer wissen wollen was eine Kundensegmentierung ist, dann können Sie dies in diesem Beitrag tun.
Diese Kundendaten nutzen wir, um mit einem K-Means-Clustering homogene Zielgruppen zu erstellen, die anschließen in Marketingkampagnen differenziert angesprochen werden können.
Das kleine Machine Learning Programm schreiben wir in Python, da Python sich als einfache Programmiersprache für ML durchgesetzt hat.
Der Datensatz
Der Datensatz erhält folgende Informationen über die Kunden: Kundennummer, Alter, Geschlecht, Einkommen und ein berechneter Score der Auskunft über das Konsumverhalten gibt. In der Praxis würde man je nach Anwendungsfall deutlich mehr Variablen nutzen. Da dies aber dieses Beispiel zu komplex macht, habe ich mich hier bewusst auf diese geringe Anzahl von Variablen beschränkt.
Hier können Sie die Daten runterladen.
In der Praxis hat man hier oft viele weitere Kundenmerkmale zu Demografie, Nutzungsverhalten und Kaufhistorie (bspw. Einkäufe in bestimmten Warengruppen).
K-Means-Algorithmus einfach erklärt
Bevor wir in das Beispiel einsteigen, möchte ich gerne noch ein paar Grundlagen zu der Clusteranalyse und dem Algorithmus erklären, den wir zur Segmentierung nutzen werden.
Was ist ein K-Means-Algorithmus?
Der K-Means-Algorithmus ist eine maschnielle Lernmethode und für die Segmentierung von Datenpunkten geeignet.
Bei einer Gruppierung (bzw. Segmentierung) wird die gesamte Datenmenge in mehrere Teilmengen bzw. Segmente unterteilt. Die Zielsetzung des K-Means-Verfahrens besteht darin, die vorliegende Datenmenge in möglichst homogene Teilmengen zu unterteilen.
Dabei werden die Informationsobjekte (z.B. Kunden) in die unterschiedlichen Gruppen (Klassen, Cluster und Segmente) eingeordnet. Die Herausforderung bei einer Gruppierung besteht darin, möglichst homogene Gruppen zu bilden. Dagegen sollten die Informationsobjekte, die sich in unterschiedlichen homogenen Gruppen befinden, möglichst unterscheiden (heterogen zwischen den Gruppen).
Häufig wird der Algorithmus auch dem Begriff des Data Mining zugeschrieben.
Wie funktioniert ein K-Means-Algorithmus?
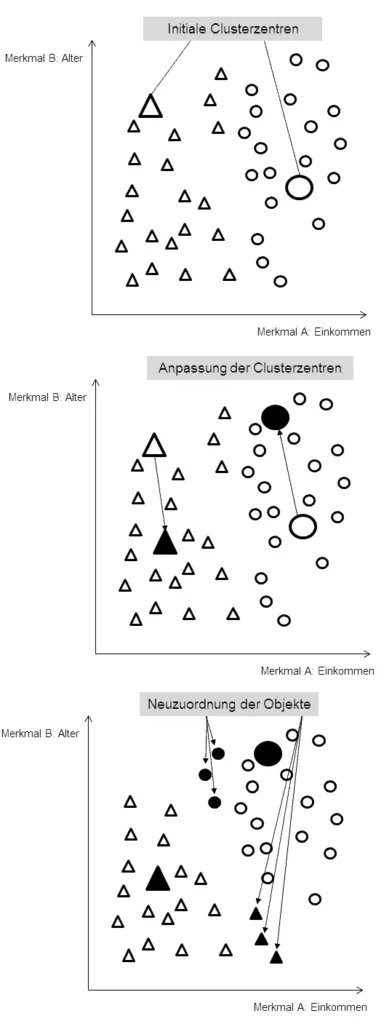
Der K-Means-Algorithmus ist ein iteratives partitionierendes Verfahren. Folgende Schritte werden durchlaufen:
- Ermittlung der Clusterzentren.
- Zuordnung der Objekte zum nächstliegenden Cluster.
- Neuberechnung der Clusterzentren durch zugeordnete Objekte.
- Wiederhole Schritt 2 und 3 bis:
- …keine Veränderung der Clusterzentren von der vorherigen Iteration zu verzeichnen ist oder
- …die maximale Anzahl der Iterationen durchlaufen ist.
Der Benutzer gibt k Cluster für das Modell vor. Die Cluster sind definiert durch die jeweiligen Clusterzentren, die durch eine separate Berechnung ermittelt werden:
Wenn die Clusterzentren ermittelt wurden, kann der K-Means-Algorithmus mit seinem iterativen Prozess beginnen.
Während der zwei- oder dreidimensionale Merkmalsraum optisch noch einfach auszudrücken ist, ist dies beim höher dimensionierten Raum nicht mehr möglich. Um die Funktionsweise des K-Means-Verfahrens zu verdeutlichen, beschränke ich mich in diesem Beispiel auf den zweidimensionalen Merkmalsraum. In der folgenden Abbildung ist die Modellerstellung anhand der Merkmale Alter und Einkommen grafisch dargestellt:
Beispiel: Clusterbasierte Kundensegmentierung mit Python
Datenexploration
Zunächst müssen wir die Daten laden und uns einen ersten Eindruck verschaffen. Die Merkmale die wir sehen sind: Kundennummer, Geschlecht, Alter, jährliches Einkommen ($k) und Konsumverhalten (als Score).
import numpy as np, pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Daten einlesen
customers = pd.read_csv('Mall_Customers.csv')
# Zeige ersten 5 Zeilen
customers.head()
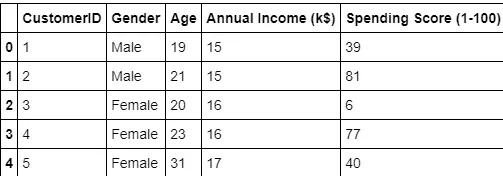
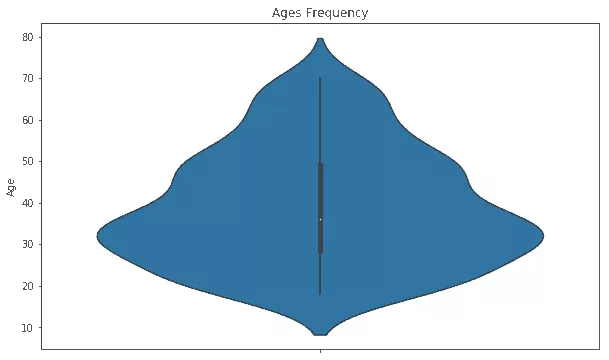
Da wir die Daten bereits in einem Flatfile haben, brauchen wir die Kundennummer nicht weiter. Lassen Sie uns einen Blick auf die Altersverteilung der Kunden werfen.
df.drop(["CustomerID"], axis = 1, inplace=True)
# Altersverteilung plotten
plt.figure(figsize=(10,6))
plt.title("Ages Frequency")
sns.axes_style("dark")
sns.violinplot(y=df["Age"])
plt.show()
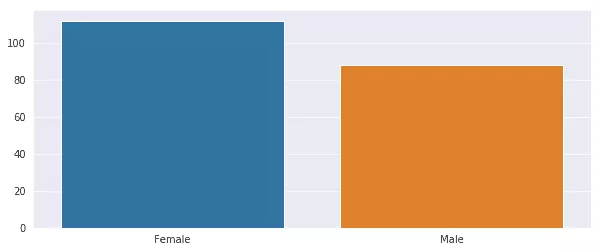
Die folgenden Balkendiagramme zeigen schön, dass wir in unserem Datenset mehr Frauen als Männer haben. Interessantes Wissen, wenn wir diese Daten später in der Kundensegmentierung nutzen.
genders = df.Gender.value_counts()
sns.set_style("darkgrid")
plt.figure(figsize=(10,4))
sns.barplot(x=genders.index, y=genders.values)
plt.show()
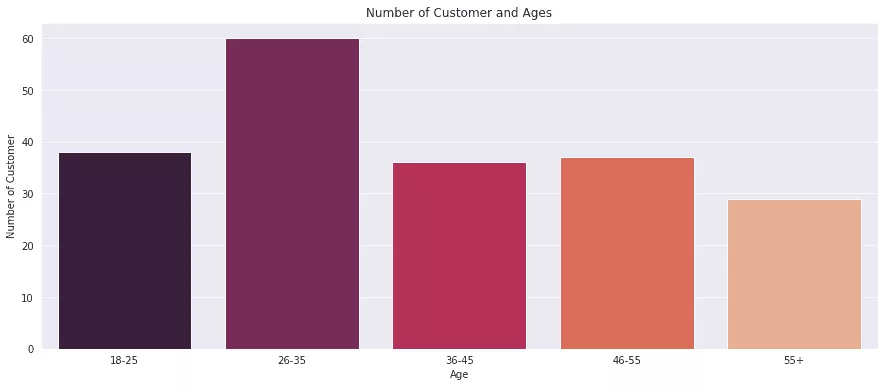
Auch für die Variable Alter habe ich ein Balkendiagramm angefertigt, dazu habe ich die Kunden in 5 Gruppen eingeteilt. Diese Gruppen nutzen wir später in unserem Algorithmus. Beim Kundenalter ist besonders die Gruppe 26-35 stark vertreten.
age18_25 = df.Age[(df.Age <= 25) & (df.Age >= 18)]
age26_35 = df.Age[(df.Age <= 35) & (df.Age >= 26)]
age36_45 = df.Age[(df.Age <= 45) & (df.Age >= 36)]
age46_55 = df.Age[(df.Age <= 55) & (df.Age >= 46)]
age55above = df.Age[df.Age >= 56]
x = ["18-25","26-35","36-45","46-55","55+"]
y = [len(age18_25.values),len(age26_35.values),len(age36_45.values),len(age46_55.values),len(age55above.values)]
plt.figure(figsize=(15,6))
sns.barplot(x=x, y=y, palette="rocket")
plt.title("Number of Customer and Ages")
plt.xlabel("Age")
plt.ylabel("Number of Customer")
plt.show()
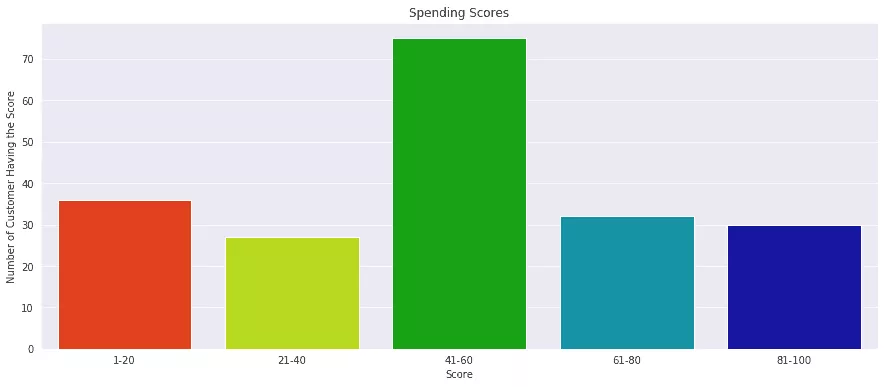
Die selben Balkendiagramme habe ich auch für das Konsumverhalten (Spending Score) angefertigt. Besonders die Gruppe 41-60 Scorepunkte, ist hier stark vertreten. Diese Informationen sind wichtige Hinweise für unseren Cluster-Algorithmus, den wir zur Kundensegmentierung nutzen.
ss1_20 = df["Spending Score (1-100)"][(df["Spending Score (1-100)"] >= 1) & (df["Spending Score (1-100)"] <= 20)]
ss21_40 = df["Spending Score (1-100)"][(df["Spending Score (1-100)"] >= 21) & (df["Spending Score (1-100)"] <= 40)]
ss41_60 = df["Spending Score (1-100)"][(df["Spending Score (1-100)"] >= 41) & (df["Spending Score (1-100)"] <= 60)]
ss61_80 = df["Spending Score (1-100)"][(df["Spending Score (1-100)"] >= 61) & (df["Spending Score (1-100)"] <= 80)]
ss81_100 = df["Spending Score (1-100)"][(df["Spending Score (1-100)"] >= 81) & (df["Spending Score (1-100)"] <= 100)]
ssx = ["1-20", "21-40", "41-60", "61-80", "81-100"]
ssy = [len(ss1_20.values), len(ss21_40.values), len(ss41_60.values), len(ss61_80.values), len(ss81_100.values)]
plt.figure(figsize=(15,6))
sns.barplot(x=ssx, y=ssy, palette="nipy_spectral_r")
plt.title("Spending Scores")
plt.xlabel("Score")
plt.ylabel("Number of Customer Having the Score")
plt.show()
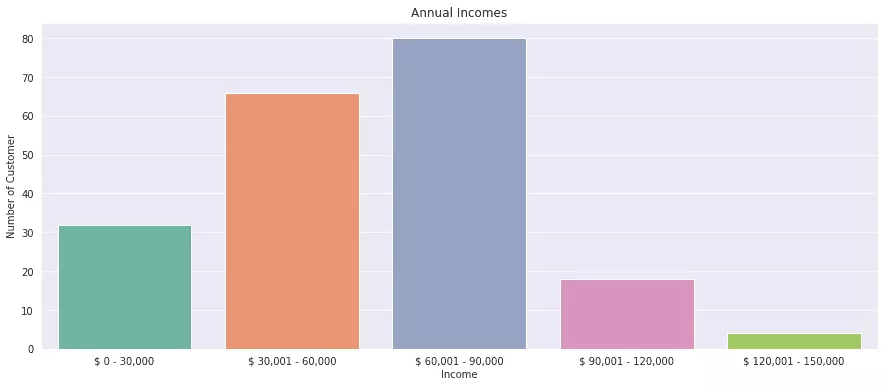
Auch das Einkommen (in tausend $ angegeben) habe ich visualisiert: deutlich zu sehen, dass die meisten Kunden ein jährliches Einkommen zwischen 60.000 und 90.000 $ haben.
ai0_30 = df["Annual Income (k$)"][(df["Annual Income (k$)"] >= 0) & (df["Annual Income (k$)"] <= 30)]
ai31_60 = df["Annual Income (k$)"][(df["Annual Income (k$)"] >= 31) & (df["Annual Income (k$)"] <= 60)]
ai61_90 = df["Annual Income (k$)"][(df["Annual Income (k$)"] >= 61) & (df["Annual Income (k$)"] <= 90)]
ai91_120 = df["Annual Income (k$)"][(df["Annual Income (k$)"] >= 91) & (df["Annual Income (k$)"] <= 120)]
ai121_150 = df["Annual Income (k$)"][(df["Annual Income (k$)"] >= 121) & (df["Annual Income (k$)"] <= 150)]
aix = ["$ 0 - 30,000", "$ 30,001 - 60,000", "$ 60,001 - 90,000", "$ 90,001 - 120,000", "$ 120,001 - 150,000"]
aiy = [len(ai0_30.values), len(ai31_60.values), len(ai61_90.values), len(ai91_120.values), len(ai121_150.values)]
plt.figure(figsize=(15,6))
sns.barplot(x=aix, y=aiy, palette="Set2")
plt.title("Annual Incomes")
plt.xlabel("Income")
plt.ylabel("Number of Customer")
plt.show()
Clusteranalyse mit K-Means
Zurück zu unserem Beispiel: Wir haben eingangs gelernt, dass wir als Benutzer, die Anzahl der Cluster (Segmente) festlegen müssen. Doch wie finden wir die optimale Anzahl von Segmenten?
Dazu gibt es die Elbow-Methode, wo berechnet wird, inwieweit ein weiteres Cluster die Distanzen innerhalb des Cluster minimiert. Daran kann man relativ einfach erkennen, was eine gute Anzahl an Clustern ist.
from sklearn.cluster import KMeans
wcss = []
for k in range(1,11):
kmeans = KMeans(n_clusters=k, init="k-means++")
kmeans.fit(df.iloc[:,1:])
wcss.append(kmeans.inertia_)
plt.figure(figsize=(12,6))
plt.grid()
plt.plot(range(1,11),wcss, linewidth=2, color="red", marker ="8")
plt.xlabel("K Value")
plt.xticks(np.arange(1,11,1))
plt.ylabel("WCSS")
plt.show()
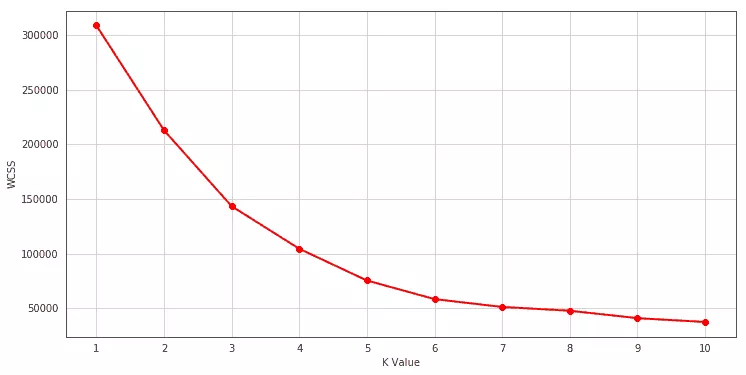
Die Kennzahl heißt Within Cluster Sum Of Squares (WCSS) und durch die Visualisierung mit der Anzahl der Cluster, bekommen wir einen guten Eindruck über die optimale Anzahl von Clustern.
Kundensegmente
Wir wissen jetzt, dass 5 Cluster eine gute Einstellung für unsere Kundensegmentierung ist.
km = KMeans(n_clusters=5)
clusters = km.fit_predict(df.iloc[:,1:])
df["label"] = clusters
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
fig = plt.figure(figsize=(20,10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(df.Age[df.label == 0], df["Annual Income (k$)"][df.label == 0], df["Spending Score (1-100)"][df.label == 0], c='blue', s=60)
ax.scatter(df.Age[df.label == 1], df["Annual Income (k$)"][df.label == 1], df["Spending Score (1-100)"][df.label == 1], c='red', s=60)
ax.scatter(df.Age[df.label == 2], df["Annual Income (k$)"][df.label == 2], df["Spending Score (1-100)"][df.label == 2], c='green', s=60)
ax.scatter(df.Age[df.label == 3], df["Annual Income (k$)"][df.label == 3], df["Spending Score (1-100)"][df.label == 3], c='orange', s=60)
ax.scatter(df.Age[df.label == 4], df["Annual Income (k$)"][df.label == 4], df["Spending Score (1-100)"][df.label == 4], c='purple', s=60)
ax.view_init(30, 185)
plt.xlabel("Age")
plt.ylabel("Annual Income (k$)")
ax.set_zlabel('Spending Score (1-100)')
plt.show()
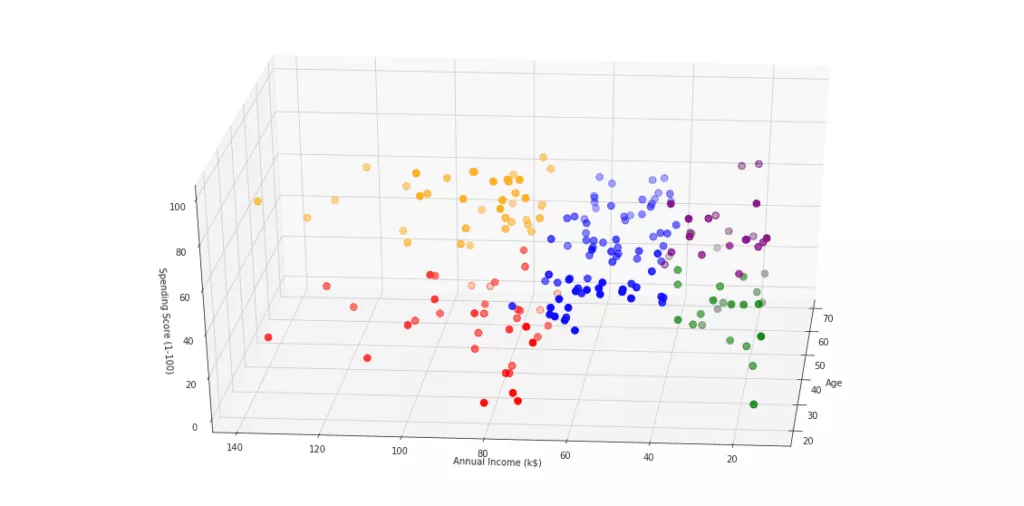
Wie sich optisch erkennen lässt, sind unsere 5 Kundensegmente in ihrem Verhalten durchaus verschieden. An diesem einfachen 3-dimensionalen Beispiel kann man deutlich sehen, dass eine Kundensegmentierung mit einem maschinellen Lernansatz, wie K-Means, Sinn macht. Ohne Algorithmus würde man schon bei 3 Merkmalen Probleme bekommen, die Kunden richtig zu segmentieren.
Nun könnte man die 5 Kundensegmente genauer beschreiben, um gezielte Marketingkampagnen zu erstellen oder das Produktsortiment den Kundensegmenten anzupassen.
Sind Sie interessiert an einer professionellen Kundensegmentierung durch maschinelles Lernen? Wenn ja, dann melden Sie sich einfach bei uns.
PS: ich habe bereits einen Artikel über 5 wertvolle Tipps für erfolgreiche Kundensegmentierungen geschrieben.